Submitting
The following classes must be submitted in order to be graded:
Make sure when you submit, all of the following are present and functional:
Class: MapMarkovModel
Constructor: MapMarkovModel()
Method: public void initialize(Scanner)
Method: protected String makeNGram(int, int)
Method: protected int readChars(Scanner)
Method: public void process(Object)
Class: WordNgram
Constructor: WordNgram(String[], int, int)
Constructor: WordNgram(String[])
Method: public boolean equals(Object)
Method: public String toString()
Method: public int hashCode()
Method: public int compareTo(WordNgram)
Class: WordMarkovModel
Constructor: WordMarkovModel()
Method: public void initialize(Scanner)
Method: protected String makeNGram(int, int)
Method: protected int readChars(Scanner)
Method: public void process(Object)
You also must submit your README in order to receive any credit.
You may create any new classes required for the above classes to compile but you must submit those as well.
The following classes should be considered “read-only” and not changed - if you submit any of them, the grader will replace them with the unmodified version you snarfed. Thus, you are free to modify them for testing, but the classes you submit should not depend on those modifications in order to be compile/have the correct return values:
A Brute Force Approach
Below is pseudo-code to generate random letters (and thus random text) using an order-k Markov model and a training text from which the probabilities are calculated.
seed = random k-character substring from the training text
repeat N times to generate N random letters
for each occurrence of seed in training text
record the letter that follows the occurrence of seed in a list
(or if end-of-file follows, record end-of-file)
choose a random element of the list as the generated letter C
if C is end-of-file, exit loop
print or store C
seed = (last k-1 characters of seed) + C
Here is the Java code implementation of this brute-force approach to generate up to maxLetters letters at random from the training-text in instance variable myString using an order-k Markov model (this is taken directly from MarkovModel.java)
protected String makeNGram(int k, int maxLetters) {
// Appending to StringBuilder is faster than appending to String
StringBuilder build = new StringBuilder();
// Pick a random starting index
int start = myRandom.nextInt(myString.length() - k + 1);
String seed = myString.substring(start, start + k);
ArrayList
// generate at most maxLetters characters
for (int i = 0; i < maxLetters; i++) {
list.clear();
int pos = 0;
while ((pos = myString.indexOf(seed, pos)) != -1 && pos < myString.length()) {
if (pos + k >= myString.length())
list.add((char) 0); //This represents the end of the file
else
list.add(myString.charAt(pos + k));
pos++;
}
int pick = myRandom.nextInt(list.size());
char ch = list.get(pick);
if (ch == 0) //end-of-file
return build.toString();
build.append(ch);
seed = seed.substring(1) + ch;
}
return build.toString();
}
</code>
The code above works, but to generate N letters in a text of size T the code does O(NT) work since it re-scans the text for each generated character. (O(NT) means that the running time is cNT, i.e. within a constant factor proportional to N times T).
###Why maxLetters?
One thing to note about this implementation of Markovian Text Generation is that the length of the generated text can vary. We specify an upper bound for the number of characters via the argument maxLetters, but if the end-of-file case is reached before we reach the upper bound, we will generate less than maxLetters characters.
This is an implementation choice - there are several ways we could guarantee that a fixed number of characters are generated:
MapMarkovModel
You’ll implement a class named MapMarkovModel that extends the abstract class AbstractModel. You should use the existing MarkovModel class to get ideas for your new MapMarkovModel class. In order to be graded your MapMarkovModel should implement a protected String makeNGram(int, int) method like MarkovModel’s which generates Ngrams.
You can modify MarkovMain to use MapMarkovModel by simply changing one line.
public static void main( String[] args) {
IModel model = new MapMarkovModel(); // THE ONLY CHANGE
SimpleViewer view = new SimpleViewer("Compsci 201 Markovian Text" +
" Generation", "k count>");
view.setModel(model);
}
Instead of scanning the training text N times to generate N random characters, you’ll first scan the text once to create a structure representing every possible k-gram used in an order-k Markov Model. You may want to build this structure in its own method before generating your N random characters. You should also note that if you generate random text more than once with the same value of k, you will not need to regenerate this structure and doing so will cost you points.
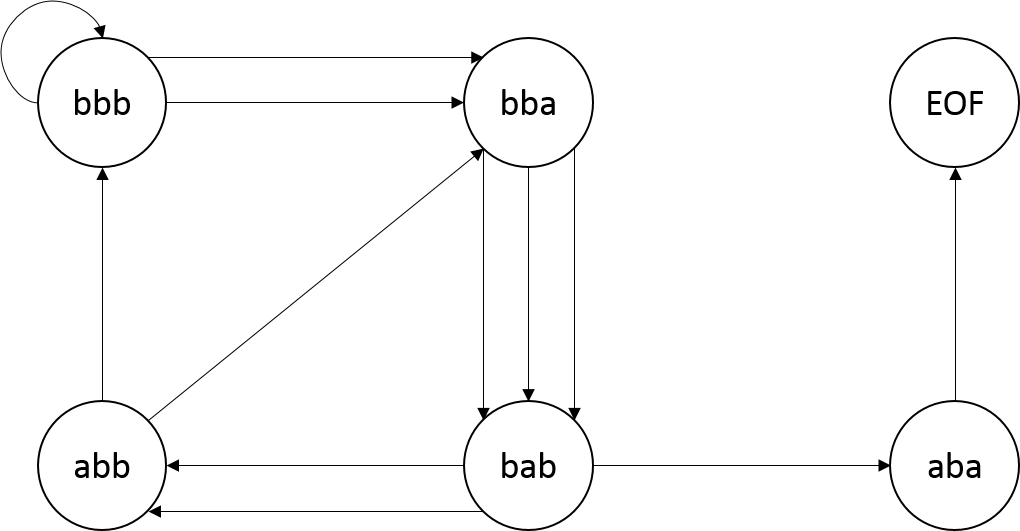
####Example Suppose the training text is “bbbabbabbbbaba” and we’re using an order-3 Markov Model.
The 3-letter string (3-gram) “bbb” occurs three times, twice followed by ‘a’ and once by ‘b’. We represent this by saying that the 3-gram “bbb” is followed twice by “bba” and once by “bbb”. That is, the next 3-gram is formed by taking the last two characters of the seed 3-gram “bbb”, which are “bb” and adding the letter that follows the original 3-gram seed.
The 3-letter string “bba” occurs three times, each time followed by ‘b’. The 3-letter string “bab” occurs three times, followed twice by ‘b’ and once by ‘a’. What about the 3-letter string “aba”? It only occurs once, and it occurs at the end of the string, and thus is not followed by any characters. So, if our 3-gram is ever “aba” we will always end the text with that 3-gram. If instead, there were one instance of “aba” followed by a ‘b’ and another instance at the end of the text, then if our current 3-gram was “aba” we would have a 50% chance of ending the text.
To represent this special case in our structure, we say that “aba” here is followed by an end-of-file (EOF) character. If while generating text, we randomly choose the end-of-file character to be our next character, then instead of actually adding a character to our text, we simply stop generating new text and return whatever text we currently have. For this assignment, to represent an end-of-file character we suggest you use the character whose integer value is 0, which can be generated using ((char) 0) – see MarkovModel’s makeNgram method for a better idea of how to implement this.
In processing the training text from left-to-right we see the following transitions between 3-grams starting with the left-most 3-gram “bbb”
bbb -> bba -> bab -> abb -> bba -> bab -> abb ->bbb -> bbb -> bba -> bab -> aba
This can be represented as a map of each possible 3gram to the 3grams that follow it (or EOF if the 3gram is at the end):

Or as a flow diagram (more formally known as a state diagram):
####Your Code
In your code you’ll replace the brute-force re-scanning algorithm for generating random text based on characters with code that builds a data structure that you’ll then use to follow the state transitions diagrammed above. Specifically, you’ll create a map to make the operation of creating random text more efficient.
Keys in the map are k-grams in a k-order Markov model. The value associated with each key is a list of related k-grams. Each different k-gram in the training text will be a key in the map. The value associated with a k-gram key is a list of every k-gram that follows key in the training text.
The list of k-grams that constitute a value should be in order of occurrence in the training text. That is, you should start generating your list of following grams from the beginning of your training text. See the table of 3-grams above as an example using the training text “bbbabbabbbbaba”. Note that the 3-gram key “bbb” would map to the list [“bba”, “bbb”, “bba”], the 3-gram key “bba”would map to the list [“bab”, “bab”, “bab”], and the 3-gram key “abb” would map to the list [“bba”, “bbb”]
Just like in the brute method, to generate random text your code should generate an initial seed k-gram at random from the training text, exactly as in the brute-force approach. Then use the pseudo-code outlined below.
// (key) --- the initial seed
seed = random k-character substring (k-gram) from the training text repeat N times to generate N random letters find the list (value) associated with seed (key) using the map next-k-gram = choose a random k-gram from the list (value) if next k-gram is EOF exit loop print or store C, the last character of next-k-gram seed = next-k-gram // Note this is (last k-1 characters of seed) + C
Construct the map once — don’t construct the map each time the user tries to generate random text unless the value of k in the order-k Markov model has changed or the training text has changed.
####Testing Your New Model
To test that your code is doing things faster and not differently you can use the same text file and the same markov-model. If you use the same seed in constructing the random number generator used in your new model, you should get the same text, but your code should be faster. Do not change the given random seed. If you do it may hurt you when your assignment is being graded. You’ll need to time the generation for several text files and several k-orders and record these times with your explanation for them in the Analysis you submit with this assignment.
Use the JUnit tests in the MarkovModelTest class to begin testing your code. You will need to change the class being tested (myMark) from MarkovModel to MapMarkovModel.
####Debugging Your Code
It’s hard enough to debug code without random effects making it harder. In the MarkovModel class you’re given the Random object used for random-number generation is constructed thusly:
myRandom = new Random(RANDOM_SEED);
RANDOM_SEED is defined to be 1234. Using the same seed to initialize the random number stream ensures that the same random numbers are generated each time you run the program. Removing RANDOM_SEED and using new Random() will result in a different set of random numbers, and thus different text, being generated each time you run the program. This is more amusing, but harder to debug. If you use a seed of RANDOM_SEED in your smart/Map model you should get the same random text as when the brute-force method is used. This will help you debug your program because you can check your results with those of the code you’re given which you can rely on as being correct.
When you submit your assignment, your code should use RANDOM_SEED as the argument to the Random. If you don’t, you will fail some of the automated tests.
WordMarkovModel
The only difference between the MapMarkovModel and the WordMarkovModel is that the MapMarkovModel operates on a character-by-character basis (a 3-gram is three characters). The WordMarkovModel operates on a word-by-word basis (a 3-gram is three words). This will be done using the WordNgram class which has been started for you.
####The WordNgram Class
The WordNgram class has been started for you. You can create new constructors or change the constructor given, though the provided constructor will likely be useful. You can also add instance variables in addition to myWords.
You’ll need to ensure that .hashCode, .equals, .compareTo and .toString work properly and efficiently. You should compare two WordNgrams like you would two String - go element-by-element, until you find a differing element, and then return a value based on that difference. Here, the elements are Strings instead of words.
You’ll probably need to implement additional methods to extract state (words) from a WordNgram object. In my code, for example, I had at least two additional methods to get information about the words that are stored in the private state of a WordNgram object.
To facilitate testing your .equals and .hashcode methods a JUnit testing program is provided. You should use this, and you may want to add more tests to it in testing your implementation. The given tests are a good indication of how well your code works, but as always JUnit tests are not a 100% guarantee.
Testing with JUnit shows that a method passes some test, but the test may not be complete. For example, your code will be able to pass the the tests for .hashCode without ensuring that objects that are equal yield the same hashvalue. That should be the case, but it’s not tested in the JUnit test suite you’re given.
####Using JUnit
To test your WordNgram class you’re given testing code. This code tests individual methods in your class, these tests are called unit tests and so you need to use the standard JUnit unit-testing library with the WordNgramTest.java file to test your implementation.
To choose Run as JUnit test first use the Run As option in the Run menu as shown on the left below. You have to select the JUnit option as shown on the right below. Most of you will have that as the only option.
There are two tests in WordNgramTest.java: one for the correctness of .equals and one for the “performance” of the .hashCode method.
If the JUnit tests pass, you’ll get all green as shown on the left below. Otherwise you’ll get red — on the right below — and an indication of the first test to fail. Fix that, go on to more tests. The red was obtained from the code you’re given. You’ll work to make the testing all green.
Remember, JUnit tests are not a guarantee of correctness. While failing a correctly written JUnit test indicates your class is incorrect, the opposite is not always true.
####The WordMarkovModel class
You’ll implement a class named WordMarkovModel that extends the abstract class AbstractModel class. This should be very similar to the MapMarkovModel class you wrote, but this class uses words rather than characters.
A sequence of characters was stored as a String in the code for character-oriented Markov models. For this program you’ll use ArrayLists (or arrays) of Strings to represent sequences of words used in the model.
The idea is that you’ll use 4-words rather than 4-characters in predicting/generating the next word in an order-4 word based Markov Model. You’ll need to construct the map-based WordMarkovModel and implement its methods so that instead of makeNgram generating 100 characters at random it generates 100 words at random (but based on the training text it reads). The words should be separated by single spaces, without any trailing whitespace at the beginning or end.
To get all words from a String use the String split method which returns an array. The regular expression "\\s+" (two back-slashes, followed by “s+”) represents any whitespace, which is exactly what you want to get all the words in file/string:
String[] words = myString.split(“\\s+”);
Using this array of words, you’ll construct a map in which each key, a WordNgram object, is mapped to a list of WordNgram objects — specifically the n-grams that follow it in the training text (instead of using ((char) 0) to represent the end of the file in your map, we suggest you use null). This is exactly what your MapMarkovModel did, but it mapped a String to a list of Strings. Each String represented a sequence of k-characters. In this new model, each WordNgram represents a sequence of k-words. The concept is the same.
####Comparing Words and Strings in the Different Models
In the new WordMarkovModel code you write you’ll conceptually replace Strings in the map with WordNgrams. In the code you wrote for maps and strings, calls to .substring will be replaced by calls to new WordNgram. This is because .substring creates a new String from parts of another and returns the new String. In the WordMarkovModel code you must create a new WordNgram from the array of strings, so that each key in the word-map, created by calling new, corresponds to a string created in your original program created by calling substring.
Analysis
The analysis has two parts.
####Part A
-
In this question, you will examine how the k-value/order of the model, the length of the training text, and the number of characters generated affect the runtime for the brute force code we give you. To do that, determine how long it takes for each of the following Markov trials to run:
alice.txt, k = 1, 200 characters max:
alice.txt, k = 1, 400 characters max:
alice.txt, k = 1, 800 characters max:
alice.txt, k = 5, 200 characters max:
alice.txt, k = 5, 400 characters max:
alice.txt, k = 5, 800 characters max:
alice.txt, k = 10, 200 characters max:
alice.txt, k = 10, 400 characters max:
alice.txt, k = 10, 800 characters max:
hawthorne.txt, k = 1, 200 characters max:
hawthorne.txt, k = 1, 400 characters max:
hawthorne.txt, k = 1, 800 characters max:
-
Based on these results, what is the relationship between the runtime and the length of the training text, the k-value, and the max characters generated? How long do you think it will take to generate 1600 random characters using an order-5 Markov model when the The Complete Works of William Shakespeare is used as the training text — our online copy of this text contains roughly 5.5 million characters. Justify your answer — don’t test empirically, use reasoning.
-
Provide timings using your Map/Smart model for both creating the map and generating 200, 400, 800, and 1600 character random texts with an order-5 Model and alice.txt. Provide some explanation for the timings you observe.
-
Provide timings for the WordMarkovModel with different hashcode methods. Time the method you are given and compare the results that you achieve with the better hashcode method that you developed.
-
Using a k of your choice and clinton-nh.txt as the training text, if we do not set a maximum number of characters generated (you can effectively do this by having maxLetters be a large number, e.g. 1000 times the size of the training text) what is the average number of characters generated by our Markov text generator?
####Part B
The goal of the second part of the analysis is to analyze the performance of WordMarkovModel using a HashMap (and the hashCode function you wrote) and a TreeMap (and the compareTo function you wrote). The main difference between them should be their performance as the number of keys (i.e, WordNGrams as keys in your map) gets large. So set up a test with the lexicons we give you and a few of your own. Figure out how many keys each different lexicon generates (for a specific number sized n-gram). Then generate some text and see how long it takes. Graph the results. On one axis you’ll have the number of keys, on the other you’ll have the time it took to generate a constant number of words (you decide - choose something pretty big to get more accurate results). Your two lines will be HashMap and TreeMap. Try to see if you can see any differences in their performance as the number of NGrams in the map get large. If you can’t, that’s fine. Provide some data values, a description of the shape of the graph, and an analysis in your README.txt.
Grading
Testing
When autograding MapMarkovModel and WordMarkovModel, we will call initialize() from your model on a Scanner, and then test the output by calling process() and then calling/using the output from makeNgram(). We will never call the methods out of this order, so you do not have to program them to handle edge cases that would occur when calling them out of order. As long as you follow the way MarkovModel’s methods handle calls, you should easily pass most tests.
For transparency’s sake, below is a list of aspects of your code the automated tests will check. Your code will still be checked by a TA, and passing all these tests does not guarantee a perfect grade.
- Do MapMarkovModel and WordMarkovModel's makeNgram generate the correct Ngram? (We test if you get the exact Ngram our solution gets, but if you don't we have a bunch of other tests to see how close/correct yours is)
- Do MapMarkovModel and WordMarkovModel's makeNgram handle the end of file correctly?
- Do MapMarkovModel and WordMarkovModel's makeNgram take less time to generate text if k and the training text take the same time?
- Do MapMarkovModel and WordMarkovModel handle a change in training text correctly?
- Do MapMarkovModel and WordMarkovModel use static variables unnecessarily?
- Do WordNgram's compareTo, equals, and hashCode methods work as expected?
- Do WordNgram's compareTo and equals handle edge cases? (Like passing a non-WordNgram to equals, or comparing two WordNgrams of different lengths)
In addition, if your code throws unexpected errors or takes too long to run the tests, you will be considered as failing the tests.
Grading
This assignment is worth 35 points.
- 67.5% Correctness: for your implementation of MapMarkovModel, WordMarkovModel, and WordNgram and passing the tests described above.
- 20% Analysis: for your README and description of the tradeoffs.
- 12.5% Engineering: for your the structure and style of your code and the implementation of the WordNgram class and its associated model. Do you appropriately use decomposition and inheritance to avoid duplicate code? </ul>
FAQs
####How should we implement WordNgram’s compareTo()?
Compare WordNgrams like you would Strings. For comparing “abc” and “abd” for example, we compare the first letters and see they’re the same, so we’d move on. We’d do the same thing for the second letter. Once we get to the third letter, we realize c and d are not the same, and c comes before d, so “abc” comes before “abd”. We could apply a similar process to the WordNgrams [“a”, “b”, “c”] and [“a”, “b”, “d”], but also to [“apple”, “bat”, “cat”] and [“apple”, “bat”, “dog”].
Also, consider comparing “ab” and “abc” and how that might translate to WordNgrams.
####Do we need to account for the case where k doesn’t change but myString does?
Yes, absolutely. If I use k = 3 and the training text “ababab”, and then k = 3 and the training text “aaaaaa”, it won’t make sense for me to receive Markov text with a ‘b’ in it for the second case, but that’s what will happen if changes to myString but not to k do not rebuild the map.
####When writing MapMarkovModel, should I start from scratch or use MarkovModel?
We suggest you use MarkovModel as a basis for MapMarkovModel. Specifically, if you declare MapMarkovModel as follows:
public class MapMarkovModel extends MarkovModel
Then any method which you don’t rewrite in MapMarkovModel, MapMarkovModel will copy from MarkovModel. This reduces the total amount of code you write without losing any functionality. If you do rewrite a method in MapMarkovModel, it is considered good style (but it is not necessary) to add an @Override annotation before the method declaration.
####When I ran my model on a large text file, it gave me an java.lang.OutOfMemoryError. How can I fix this?
In the Eclipse menu, click on Run -> Run configurations, and add -Xmx512M (or -Xmx1024M, -Xmx2048M) under VM arguments to increase the size of your heap.
If you still get the error after adding VM arguments, you are likely using too much memory somehow (e.g. storing maps you don’t need anymore).
You need to be able to run on large text files, otherwise you may fail tests where we compare the results of your model to the results of our model on large text files.
####For MapMarkovModel, I know I can compare the results to the brute-force model by using the same random seed, but how do I verify the results from WordMarkovModel?
Try writing your own text file which has predictable results (hint: if you add a space between every character in a one-word text file, how would the output of MapMarkovModel using the original text and the output of WordMarkovModel using the modified text compare?)
Alternatively, as long as you do not look at each others code, you and a classmate are free to share the outputs of your models on certain text files and compare. Chances are if you and 1 or 2 classmates generate the same results, you are all correct.
####Am I allowed to add methods to any of the classes I am writing other than the ones specified?
Yes! Breaking up your code using helper methods and making classes more functional by adding various methods is never a bad thing. In fact, you will definitely need to add a method to WordNgram, and MapMarkovModel/WordMarkovModel will be much easier with a helper method.
That being said, keep in mind some of the classes we’ve given you shouldn’t be modified. See the submitting guidelines for more info.
####How do I combine all the words in WordMarkovModel’s output?
The output string should have all the words, separated by one space each, with no trailing space. So, if the words produced were [“a”, “b”, “c”], the output String should be “a b c”. Make sure you don’t have any trailing spaces! (like “a b c “).
If you’re using Java 8, one method you could use is String.join(). Alternatively, every time you add a word to your output, add a space after it. Then, before returning, trim the space off using String.trim().
####How should I handle punctuation in WordMarkovModel?
There’s no need to treat punctuation characters specially, just treat them like any other character. This means that “end” and “end.” should be different words just like “end” and “ends” are. The only characters you need to worry about are whitespace characters, which .split("\\s+") will handle for you.
####Why do I get a ArrayIndexOutOfBoundsException?
You’re attempting to access an element outside the bounds of an array. e.g. For a 10-element array, arr, arr[x] will trigger this exception for x < -1 and x > 10.
When students get this exception in this project, it is usually a result of an off-by-one error in a for loop. It also often occurs as a result of initializing WordNgram, which uses arrays in its constructor, without understanding how the arguments to the constructor are used - reading that constructor may help you avoid this error.
####Why do I get a NullPointerException?
NullPointerExceptions occur when either a method is passed a null value and that method rejects it, or you try to call something from a null value. e.g. a TreeMap will throw a NullPointerException if you try to call TreeMap.get(null). Alternatively, if a is null, then calling something like a.hashCode() will throw a NullPointerException even though hashCode is not written to throw one.
As a note, for any map, if you do not put a key into it but attempt to get the value associated with that key, you will get null. So, the following code would throw an exception:
HashMap<String, String> markovMap = new HashMap<String, String>();
String gram = markovMap.get("a");
System.out.println(gram.hashCode());
Markov
##Markov - Overview

######Markov text generated at what-would-i-say using the Duke Facebook page as a training source
Welcome to the Markov assignment. In this assignment, you will be using the Markovian Text Generation algorithm to generate random text modeled after some source. In doing so, you will learn how data structures like maps can make code more efficient, and get experience writing and implementing your own class in Java.
Here is a printer friendly version of this assignment.
The code for this assignment is available through Snarf (using Ambient), or the equivalent .jar can be downloaded from here.
You can also view/download the individual classes:
###Acknowledgements
Joe Zachary developed this nifty assignment in 2003 and Kevin Wayne and Robert Sedgewick have been using pseudo-random text generation as the basis for an assignment since 2005 and possibly earlier. Owen Astrachan created the original Duke version.
###Introduction An order-k Markov model uses strings of k-letters to predict text, these are called kgrams.
An order-2 Markov model uses two-character strings or bigrams to calculate probabilities in generating random letters. For example suppose that in some text that we’re using for generating random letters using an order-2 Markov model, the bigram “th” is followed 50 times by the letter ‘e’, 20 times by the letter ‘a’, and 30 times by the letter ‘o’, because the sequences “the”, “tha” and “tho” occur 50, 20, and 30 times, respectively while there are no other occurrences of “th” in the text we’re modeling.
Now suppose that we want to generate random text. We generate the bigram “th” and based on this we must generate the next random character using the order-2 model. The next letter will be an ‘e’ with a probability of 0.5 (50/100); will be an ‘a’ with probability 0.2 (20/100); and will be an ‘o’ with probability 0.3 (30/100). If ‘e’ is chosen, then the next bigram used to calculate random letters will be “he” since the last part of the old bigram is combined with the new letter to create the next bigram used in the Markov process.
###Assignment Overview You will have four primary tasks for this assignment.
- Make the provided class MarkovModel faster (by writing a new model MapMarkovModel, not changing the existing model)
- Implement the WordNgram class.
- Use the WordNgram class to create a new, word-based Markov Model.
- Perform empirical analysis on the different implementations.
After you snarf the assignment run MarkovMain, the brute-force Markov generator. Using the GUI, go to File -> Open File and select a data file to serve as the training text. There is a data directory provided when you snarf containing several files you can use as training texts when developing your program.