Submitting
The following classes must be submitted in order to be graded:
- PercolationDFS.java
- PercolationStats.java
- PercolationUF.java
- PercolationVisualizer.java
- QuickUWPC.java
Make sure when you submit, all of the following are present and functional:
Class: PercolationDFS
Constructor: PercolationDFS(int)
Method: public void open(int, int)
Method: public boolean isOpen(int, int)
Method: public boolean percolates()
Method: public boolean isFull(int, int)
Class: PercolationUF
Constructor: PercolationUF(int, IUnionFind)
Method: public void open(int, int)
Method: public boolean isOpen(int, int)
Method: public boolean percolates()
Method: public boolean isFull(int, int)
Class: PercolationStats
Method: public static void main(String[])
Class: PercolationVisualizer
Method: public static void main(String[])
Class: QuickUWPC
Method: public void initialize(int)
Method: public int components()
Method: public int find(int)
Method: public boolean connected(int, int)
Method: public void union(int, int)
You also must submit your README in order to receive any credit.
If you create any new classes which are required for the above classes to compile, you should submit those as well.
The classes we give you which are not specified above should be considered “read-only” - if you submit them, the grader will replace them with the unmodified version you snarfed. Thus, you are free to modify them for testing, but the classes you submit should not depend on those modifications in order to be compile/have the correct return values.
PercolationDFS/PercolationUF
###IPercolate data type To model a percolation system, you will create different implementations of the IPercolate interface:
public interface IPercolate {
// Opens site at (row i, col j) if it is not already open
public abstract void open(int i, int j);
// Returns true if and only if site (row i, col j) is OPEN
public abstract boolean isOpen(int i, int j);
// Returns true if and only if site (row i, col j) is FULL
public boolean isFull(int i, int j);
// Returns true iff the simulated system percolates
public abstract boolean percolates();
}
You will complete brute-force (PercolationDFS) and union-find (PercolationUF) versions of the IPercolate data type.
NB
- By convention, the indices i and j are integers between 0 and N-1, where (0, 0) is the upper-left cell. Your code must follow this convention in order to pass our tests.
- The methods can be called in any order. That is, you could call percolates twice in a row and then isFull, so make sure that your methods will return the correct value given the current state of your IPercolate object.
Below are some tips to get you started (not all methods you need to write have tips). Some tips for PercolationUF may be invalid if you are attempting the extra credit.
It may be useful to define and use constants (e.g. globals named OPEN, FULL, BLOCKED, probably ints) to keep track of the state of each cell.
####Constructor
Be sure to initialize your grid to be completely blocked.
####Open
See DFS below
####IsOpen and IsFull
These should both be one-line, O(1) methods. For our solution, cells which are full are not considered open by isOpen. That is, isFull(i, j) and isOpen(i, j) cannot both be true at the same time.
####DFS
This method should use DFS from the top of the grid to determine which cells are filled and update myGrid.
Every cell this method visits should be marked as filled. Recursive calls should only be made on adjacent cells which are open (we avoid infinite recursion by not revisiting full cells) - because of this, make sure to flush the grid by marking all full cells as open before calling this method, otherwise the method will stop immediately and not explore the grid.
Since the purpose of dfs is to update the status of each cell, and each cell’s status can only change when a new cell is opened, you want to call this method only when open is called.
For the purposes of analysis - a depth-first-search that visits k sites with m total connections between them takes O(k+m). Here, the sites are the cells in the grid, and the connections are the edges between two adjacent cells. This should let you determine the runtime of calling this method on all the top cells (we can consider all the calls to dfs made from one call to open as one search, since they cumulatively will not visit the same cell twice)
Be sure to handle out-of-bounds cases correctly in all methods.
Your IUnionFind object should have two additional elements besides those representing cells - a virtual source and virtual sink representing the top and bottom of the Percolation object. Be sure to use a consistent value for the index of these (constants may help here).
####Open
You should be making union calls in this method or in a helper method called by this method. Remember to handle unions for top/bottom cells with a special case.
####isOpen and isFull
These should both be one-line, O(1) methods. Unlike PercolationDFS, for our solution, cells which are considered full by isFull are also considered open by isOpen. That is, if isFull(i, j) is true, then isOpen(i, j) must be true.
This may seem confusing, but it makes writing PercolationDFS and PercolationUF respectively much easier - for DFS, not being able to consider cells open and full at the same time is more convenient, but for union-find, the opposite is more convenient.
####Percolates
This should now be an O(1), one line method.
Percolation Visualizer
Your completed PercolationVisualizer should prompt the user for N and display the
percolation process starting with a N-by-N grid of sites (initially all
blocked and
black). After
each site is opened, display full sites in
cyan,
open sites (that aren’t full) in
white,
and blocked sites in black using
princeton.StdDraw.
Here is an example of steps in a visualization on a 20x20 grid as in this linked movie and the following snapshots.

#####Going from 50 to 100 to 150 to 204 to 250 open sites in a 20x20 grid.
You can test your code by adding a method in your PercolationVisualizer to read cells to open from a file. The first line is N and the subsequent lines are cells to open. Opening the cells in input20.txt should result in the animation shown in the movie above. You could add either add a method to PercolationVisualizer to read in the cells to open from a file. Alternatively, you could read the row and column indices from the two arrays defined below.
rowIndices = { 6, 17, 11, 8, 4, 0, 11, 4, 15, 2, 8, 11, 3, 2, 1,
4, 4, 16, 9, 3, 12, 3, 2, 7, 12, 14, 18, 18, 4, 18, 8, 6, 6, 8,
2, 1, 3, 9, 8, 9, 12, 8, 5, 7, 5, 13, 4, 3, 11, 17, 4, 14, 16,
3, 10, 10, 17, 7, 4, 1, 13, 12, 10, 10, 10, 12, 14, 5, 17, 13, 2, 7,
11, 5, 13, 10, 8, 14, 18, 14, 5, 7, 8, 9, 13, 13, 0, 10, 18, 17, 12,
17, 1, 4, 3, 3, 13, 1, 14, 19, 11, 7, 4, 17, 4, 9, 1, 4, 2, 19,
10, 15, 3, 8, 16, 13, 18, 6, 18, 10, 14, 12, 13, 10, 11, 16, 11, 0, 3,
17, 16, 12, 6, 1, 7, 18, 11, 19, 3, 14, 14, 16, 16, 0, 4, 19, 17, 2,
13, 15, 16, 18, 9, 0, 1, 14, 5, 11, 14, 17, 0, 15, 15, 18, 0, 7, 0,
18, 7, 15, 3, 14, 10, 3, 0, 3, 7, 13, 18, 17, 4, 16, 3, 6, 12, 1,
10, 15, 17, 10, 14, 14, 16, 15, 17, 17, 2, 6, 9, 13, 16, 0, 17, 6, 15,
5, 10, 11, 11, 6, 1, 12, 0, 14, 12, 16, 12, 14, 7, 18, 4, 0, 13, 5,
11, 6, 19, 8, 2, 15, 19, 6, 19, 6, 8, 7, 2, 2, 2, 4, 18, 15, 19,
4, 5, 7, 11, 1, 15, 0, 15, 0};
colIndices = { 10, 10, 4, 4, 8, 0, 0, 3, 18, 12, 13, 3, 10, 2, 1,
16, 19, 10, 2, 16, 3, 17, 3, 14, 4, 6, 19, 17, 0, 10, 9, 14, 0, 12,
11, 12, 9, 10, 0, 16, 14, 5, 4, 16, 8, 5, 9, 11, 15, 1, 10, 15, 12,
14, 2, 12, 19, 11, 5, 5, 17, 13, 6, 19, 13, 9, 16, 14, 9, 10, 0, 9,
13, 13, 9, 8, 18, 1, 5, 12, 1, 6, 8, 6, 19, 7, 13, 14, 0, 7, 7,
11, 4, 1, 6, 19, 12, 7, 11, 11, 6, 13, 4, 15, 11, 14, 6, 18, 8, 12,
7, 17, 4, 14, 9, 18, 7, 12, 11, 11, 17, 17, 0, 18, 18, 3, 5, 8, 8,
8, 18, 19, 1, 3, 10, 6, 1, 5, 15, 4, 2, 5, 11, 4, 13, 6, 6, 18,
14, 16, 14, 18, 5, 7, 8, 10, 6, 17, 3, 16, 10, 19, 3, 8, 6, 1, 12,
12, 2, 2, 1, 8, 3, 0, 14, 7, 12, 11, 13, 14, 6, 13, 5, 8, 6, 14,
0, 10, 4, 1, 14, 7, 6, 7, 0, 2, 17, 7, 13, 13, 15, 3, 12, 9, 1,
7, 5, 8, 10, 5, 2, 0, 1, 0, 15, 19, 18, 18, 0, 9, 12, 16, 4, 9,
11, 15, 18, 10, 5, 0, 0, 17, 4, 11, 1, 19, 14, 13, 4, 17, 16, 11, 3,
15, 2, 5, 14, 15, 5, 17, 5, 17};
When drawing the grid, the animation will be smoothest if you do not call StdDraw.show more than once per iteration. Otherwise, some cells may flash white before appearing blue if your IPercolate implementation allows for a cell to be open and full at the same time.
Estimating p*
To estimate the percolation threshold, perform the following computational experiment on a percolation object:
- Initialize all sites to be blocked.
- Repeat the following until the system percolates:
- Choose a blocked site (row i, column j) uniformly at random among all blocked sites.
- Open the site (row i, column j).
- The fraction of sites that are now opened provides an estimate of the percolation threshold.
To obtain an accurate estimate of the percolation threshold, repeat the experiment T times and average the results. Let xt be the fraction of open sites in experiment t. The sample mean, μ, provides an estimate of the percolation threshold. The sample standard deviation, σ, measures the sharpness of the threshold. You can calculate these values as follows (notice the right formula is for σ2):
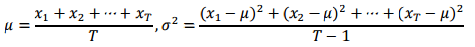
Assuming T is sufficiently large (say, at least 30), the following provides a 95% confidence interval for the percolation threshold:
You will write a client program, PercolationStats, that prompts the user for N and T, performs T independent experiments on an N-by-N grid, and prints out the 95% confidence interval for the percolation threshold. Use java.util.Random to generate random numbers and follow steps above to compute the sample mean and standard deviation. Below is an example run with N=200 and T=100.
mean percolation threshold = 0.5921
stddev = 0.0098
95% confidence interval = [0.5902, 0.5940]
total time = 2.074s
mean time per experiment = 0.02074
stddev = 0.00376
Analysis
Implement PercolationUF using the quick find data structure (QuickFind.java) and by creating a version using the weighted quick union with path compression data structure.
Adapt the code from class or WeightedQuickUnionUF.java to create
QuickUWPC.java which implements the IUnionFind interface. Run
PercolationStats to gather timings for
PercolationDFSPercolationUFwithQuickFindPercolationUFwithQuickUWPC
In your README, you will answer the following questions.
- How does doubling N affect the running time?
- How does doubling T affect the running time?
- Measure running time (using calls to System.currentTimeMillis) of the three versions of your program (DFS, Quick Find, and weighted quick union with path compression).
- Give a formula (using Big-Oh notation) of the running time on your computer (in seconds) as a function of both N and T.
- Estimate the largest experiment you could perform in one [minute, day, year] assuming your computer has enough memory.
- Give a formula (using Big-Oh notation) that describes the amount of memory (in bytes) that your IPercolate object consumes as a function of N for DFS, Quick Find, and weighted quick union with path compression).
Grading Criteria
Automated Tests
For transparency’s sake, below is a list of aspects of your code the automated tests will check. Your code will still be checked by a TA, and passing all these tests does not guarantee a perfect grade. Make sure you follow the conventions for isOpen and isFull in PercolationDFS and PercolationUF outlined in this writeup. We test your IPercolate implementations by seeing if they produce the same grid ours do, so if yours differ from ours you will fail many tests.
- Do PercolationDFS and PercolationUF's isOpen, isFull, and percolates methods return the expected values?
- Do PercolationDFS and PercolationUF handle out of bounds calls correctly?
- Do PercolationDFS and PercolationUF run percolation simulations correctly?
- Do PercolationDFS and PercolationUF work with small N?
- Do PercolationDFS and PercolationUF accept calls to open/isOpen/isFull/percolates after percolation occurs?
- Do PercolationDFS and PercolationUF use unnecessary static variables?
- Do PercolationDFS and PercolationUF handle the longest possible simulation correctly? (percolation only occurring after close to N2 opens)
- Do PercolationDFS and PercolationUF handle calls to methods in a random order correctly? (will not pass if any of your methods besides open() change values in the grid, for example)
- Do PercolationDFS and PercolationUF handle backwash correctly? (UF handling backwash is for extra credit, you can still get full credit if PercolationUF produces backwash)
- Does a trial of PercolationUF make a reasonable number of calls to the methods in the IUnionFind object?
- Does PercolationUF make a constant number of calls to IUnionFind per call to each of its methods, regardless of what N is?
- Does PercolationUF achieve a reasonable order of growth when using an optimized IUnionFind object?
In addition to the automated tests, we will
- time your IPercolate implementations,
- test whether your PercolationVisualizer draws the grid correctly for both implementations, and
- run your PercolationStats to see if it produces the correct results.
Grading Breakdown
This assignment is worth 40 points.
- 60% Correctness: for your implementation of PercolationDFS, PercolationUF, PercolationVisualizer, QuickUWPC, and PercolationStats and passing the tests described above.
- 25% Analysis: for your README, answers to the questions, and description of the tradeoffs.
- 15% Engineering: for your the structure and style of your IPercolate implementations. Is your code inefficient? For example, is the time required for percolates or open for PercolationUF proportional to N? Do you appropriately use decomposition to avoid duplicate code in PercolationVisualizer and PercolationStats? </ul>
FAQ
####What should I read prior to writing code:
Most of the code in this assignment comes from discussion in the text and supplementary reading. Please review the following:
- Section 2.4 in Introduction to Programming in Java by Robert Sedgewick & Kevin Wayne
- Sedgewick & Wayne's union-find case study or the following excerpt from Algorithms, 3rd Edition
- API documentation for princeton.StdDraw
- Optional: If you'd like to understand the theory behind the complexity of union-find operations in detail, read these notes from Robert Tarjan
>>>>>>> development
####What should stddev() return if T equals 1?
The sample standard deviation is undefined. We recommend returning
Double.NaN(Not-A-Number). ####After the system has percolated, my PercolationVisualizer colors in cyan all sites connected to open sites on the bottom (in addition to those connected to open sites on the top). Is this backwash OK?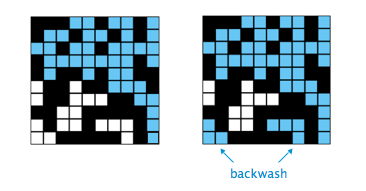 Yes, we won't deduct for that for PercolationUF (PercolationDFS should not have backwash, if it does there's a major error). You can think of the water as filling back up from the bottom.
If you finish early, you can try to eliminate backwash without using a second union-find structure or worsening the runtime's order of growth for extra credit. Our tests for PercolationUF compare your grid to both an IPercolate implementation which removes backwash and one which does not. Thus, whether or not you implement backwash should not affect your correctness score.
Your solution to eliminate backwash should be isolated within PercolationUF - that is, it should be independent of the IUnionFind implementation used and the visualizer. In addition, the Big-Oh runtime of every method should not increase as a result of implementing backwash removal, otherwise you will fail the engineering tests.
####How efficient should the methods in PercolationUF be?
For a NxN grid, the construction should take N2 time; the other methods should take time at most logarithmic in N.
####How do I generate a random blocked site?
Create a list of all blocked sites. [Shuffle](http://docs.oracle.com/javase/8/docs/api/java/util/Collections.html#shuffle-java.util.List-java.util.Random-) the list at the beginning and then each step pick the next element from the list.
####How many bytes does a data structure need?
In
computing the memory required, you should be most concerned about the
number of values stored.
An int uses 4 bytes. A double requires 8 bytes.
Yes, we won't deduct for that for PercolationUF (PercolationDFS should not have backwash, if it does there's a major error). You can think of the water as filling back up from the bottom.
If you finish early, you can try to eliminate backwash without using a second union-find structure or worsening the runtime's order of growth for extra credit. Our tests for PercolationUF compare your grid to both an IPercolate implementation which removes backwash and one which does not. Thus, whether or not you implement backwash should not affect your correctness score.
Your solution to eliminate backwash should be isolated within PercolationUF - that is, it should be independent of the IUnionFind implementation used and the visualizer. In addition, the Big-Oh runtime of every method should not increase as a result of implementing backwash removal, otherwise you will fail the engineering tests.
####How efficient should the methods in PercolationUF be?
For a NxN grid, the construction should take N2 time; the other methods should take time at most logarithmic in N.
####How do I generate a random blocked site?
Create a list of all blocked sites. [Shuffle](http://docs.oracle.com/javase/8/docs/api/java/util/Collections.html#shuffle-java.util.List-java.util.Random-) the list at the beginning and then each step pick the next element from the list.
####How many bytes does a data structure need?
In
computing the memory required, you should be most concerned about the
number of values stored.
An int uses 4 bytes. A double requires 8 bytes.
Percolation
##Percolation - Overview
Welcome to the Percolation assignment. In this assignment, you will write a program to estimate the value of the percolation threshold via Monte Carlo simulation. In doing so, you will better understand depth-first-search, union-find structures, and the use of computer simulations for statistical inquiry.
Here is a printer friendly version of this assignment.
The code for this assignment is available through Snarf (using Ambient), or the equivalent .jar can be downloaded from here.
You can also view/download the individual classes:
###Acknowledgements
The assignment was developed by Kevin Wayne at Princeton University for their Computer Science 226 class.
###Introduction
Given a composite systems comprised of randomly distributed insulating and metallic materials: what fraction of the materials need to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations.
###The Model
We model a percolation system using an N-by-N grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. (For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom.)
In a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and therefore blocked with probability 1 − p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20-by-20 random grid (left) and 100-by-100 random grid (right).
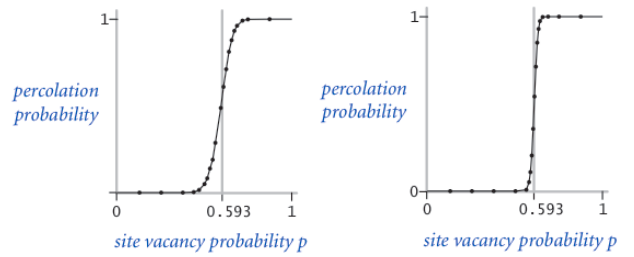
When N is sufficiently large, there is a threshold value p* such that when p < p* a random N-by-N grid almost never percolates, and when p > p*, a random N-by-N grid almost always percolates. No mathematical solution for determining the percolation threshold has yet been derived.
###The Assignment Your task is to write a program to:
- Visualize the percolation process
- Estimate p* for a square grid percolation model
- Compare brute force (depth-first search) to union-find for finding connected open sites
You need to write code for the following classes:
PercolationDFS.java: This class implements the brute force method for percolation. Please refer to Section 2.4 in the Introduction to Programming in Java. You will complete the following methods:
- constructor: initialize a grid of size n
open: open a particular grid cellisOpen&isFull: give current state of grid cellpercolatesanddfs: determine whether current grid will percolate by implementing recursive scheme depth-first search as discussed in class and the textbook
PercolationVisualizer.java: complete main so that it repeatedly calls a
percolator (i.e., something that implements IPercolate like PercolationDFS) to
declare sites open, draw, and pause until the system percolates
PercolationUF.java: You will implement a more efficient solution that can use
any union-find algorithm that implements IUnionFind (e.g., QuickFind.java). You will complete the following methods:
- constructor: initialize a grid of size n and union-find algorithm
open: open a particular grid cell and merge components as appropriateisOpen&isFull: give current state of grid cellgetIndex: return an index that uniquely identifies (row, col), so that each grid square can be in its own set at the beginningpercolates: determine whether top and bottom are connected (i.e., in the same component)
QuickUWPC.java: A class that implements the weighted quick union with path compression data structure. See the Sedgewick & Wayne case study or the following reading for more information. You will need to create this file by adapting WeightedQuickUnionUF.java to implement the IUnionFind interface.
PercolationStats.java: A class that prompts for N and T, performs T experiments on an NxN grid, and prints the mean, standard deviation, and confidence interval of the percolation threshold, and timings of percolation simulations.