Submitting
The following classes must be submitted in order to be graded:
Make sure when you submit, all of the following are present and functional:
Class: BinarySearchAutocomplete
Constructor: BinarySearchAutocomplete(String[], double[])
Method: public String topMatch(String)
Method: public String[] topKMatches(String, int)
Method: public static int firstIndexOf(Term[], Term, Comparator)
Method: public static int lastIndexOf(Term[], Term, Comparator)
Class: TrieAutocomplete
Constructor: TrieAutocomplete(String[], double[])
Method: private void add(String, double)
Method: public String topMatch(String)
Method: public String[] topKMatches(String, int)
Field: protected Node myRoot
Class: Term
Class: Term$WeightOrder
Method: public int compare(Term, Term)
Class: Term$ReverseWeightOrder
Method: public int compare(Term, Term)
Class: Term$PrefixOrder
Constructor: Term$PrefixOrder(int)
Method: public int compare(Term, Term)
Field: private final int r
Constructor: Term(String, double)
Method: public String toString()
Method: public int compareTo(Term)
You also must submit your README in order to receive any credit.
If you create any new classes which are required for the above classes to compile, you should submit those as well.
Any other classes we provide you should be considered “read-only” - if you submit them, the grader will replace them with the unmodified version you snarfed. Thus, you are free to modify them for testing, but the classes you submit should not depend on those modifications in order to be compile/have the correct return values:
The Autocomplete Algorithm
Autocomplete is an algorithm used in many modern software applications. In all of these applications, the user types text and the application suggests possible completions for that text:


While finding terms that contain a query is trivial, these applications need some way to select only the most useful terms to display (since users will likely not comb through thousands of terms, nor will obscure terms like “antidisestablishmentarianism” be useful to most users). Thus, autocomplete algorithms not only need a way to find terms that start with or contain the prefix, but a way of determining how likely each one is to be useful to the user and filtering out only the most useful ones.
According to one study, in order to be useful the algorithm must do all this in at most 50 milliseconds. Any longer, and the user will already be inputting the next keystroke (while humans do not on average input one keystroke every 50 milliseconds, additional time is required for server communication, input delay, and other processes). Furthermore, the server must be able to run this computation for every keystroke, for every user.
In this assignment, you will be implementing autocomplete using several different algorithms and seeing which ones are faster in certain scenarios. Our autocomplete will be different than the industrial examples described above in two ways:
Term Overview/Methods
The Term class serves two purposes.
- The basic purporse is to encapsulate a term-weight pair.
- More importantly, Term allows us to use Comparable and Comparator to sort terms in a variety of ways, which will make Autocompletor implementations much simpler. It is very difficult to write our Autocompletor implementations without having Term written, so you should complete this class first.
Within this class, you should:
Notice that the methods compareTo, getWord,
getWeight, and toString are already completed for
you. Most importantly, notice that compareTo sorts by lexicographic order
using the word parameter. This functionality will be utilized in
BinarySearchAutocomplete.
###The Constructor The constructor simply needs to take the input arguments and store them to the class variables. Make sure you throw the exceptions listed in the method header when required.
###WeightOrder and ReverseWeightOrder For these comparators, all you need to do is write the compare method for each of them. Remember, compare(a, b) should return a negative value when a comes before b in the desired order.
###PrefixOrder PrefixOrder is a bit more interesting. PrefixOrder is initialized with an integer argument r. PrefixOrder should sort terms lexicographically, but only using the first r letters. So, while “beeswax” comes after “beekeeper” using lexicographical sorting, the two words would be considered equal using PrefixOrder with r = 3.
For words shorter than r letters, we still use lexicographical ordering. So, “bee” still comes before “beeswax” using PrefixOrder(4), since “bee” would come before “bees” and similarly “bug” would come after “beeswax” using PrefixOrder(4) since “bees” would come before “bug” in lexicographic order.
Since only the first r letters of any word are relevant in PrefixOrder(r), for full credit PrefixOrder(r).compare(v, w) should take O(r) to run, independent of the length of v and w.
PrefixOrder may seem arbitrary and maybe even useless at first, but when
you implement BinarySearchAutocomplete, it will prove rather useful.
###After Term Is Written Once Term is written, the provided BruteAutocomplete class should be fully functional. Try setting AUTOCOMPLETOR_CLASS_NAME to BRUTE_AUTOCOMPLETE in AutocompleteMain and running it. If you load words-333333.txt and type in “auto” you should get the following result:
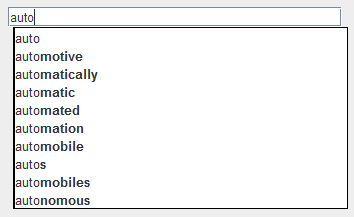
BruteAutocomplete only uses Term.WeightOrder, so getting the above result does not necessarily mean all your Comparators are working correctly.
Since the Comparators are inner classes, to initialize them in other classes, use the following syntax:
new Term.WeightOrder();
new Term.ReverseWeightOrder();
new Term.PrefixOrder(r);
BinarySearchAutocomplete Overview/Methods
BinarySearchAutocomplete
implements the Autocompletor interface, which
means it should, given a list of terms and weights for those terms, be able
to find the top match(es) for a prefix amongst those terms. To do this, you
will write binary search methods which can narrow the list of all terms
down to a list of terms matching the prefix. Once we have a list of
prefix-matching terms, finding the highest weight ones should be trivial.
Within this class, you should:
- Write the binary search method firstIndexOf
- Write the binary search method lastIndexOf
- Write the interface-required method topMatch
- Write the interface-required method topKMatches
###The Constructor
The constructor for this class is already written for you. However, you should still quickly read through it to understand what it does. Notice that the list of terms is initialized for you in lexicographic order. This means you should not need to sort it yourself - doing so will slow down your methods unnecessarily. Furthermore, you should maintain the sorted order - if one of your methods changes the array of Terms, or if methods fail because the first method call did not preserve sorted order for the second, you might lose points.
###firstIndexOf and lastIndexOf You should be comfortable with the binary search algorithm already. We will be implementing two more specific versions of it in the methods firstIndexOf and lastIndexOf. firstIndexOf and lastIndexOf are different from typical binary search algorithms in two ways:
- firstIndexOf and lastIndexOf should not check for exact equality, but rather for equality according to the Comparator argument. This is so that we can use PrefixOrder (which has a very loose definition of equality) in conjunction with binary search to narrow down the list of terms.
- firstIndexOf should return the smallest index of any matching element, and lastIndexOf should return the largest index. This means that when you find a matching element, you cannot immediately return its index as there might be matching elements with a smaller/larger index. Instead, finding an element equal to the element being searched for simply halves your range of possible indices, just like finding an element not equal to the search element. More specifically, in firstIndexOf, the index of a matching element should be your new upper bound, and in lastIndexOf, the index of a matching element should be your new lower bound.
As a performance requirement, firstIndexOf and lastIndexOf should use at most 1 + ⌉log2N⌈ compare calls for an N-element array. The methods should return -1 if no matching element exists, including the case where the input array is empty.
###topMatch and topKMatches
Once firstIndexOf and lastIndexOf are written, most of the work for topMatch and topKMatches is done. By using firstIndexOf and lastIndexOf and Term.PrefixOrder, you can easily find the indices of all terms starting with the prefix. Once you have narrowed down the list of terms to m terms starting with the prefix, finding the highest weight term(s) and returning them should be trivial.
If there are m terms starting with the prefix, the best timing for finding a top match is O(log n + m), and the best timing for the top k matches is O(log n + m log m). You should be able to justify for yourself that your methods run in these times.
One may notice that topMatch is simply a special case of topKMatches where k = 1 and be tempted to have topMatch simply call
topKMatches(prefix,1)
Do not do this – the optimal timing for topKMatches is worse than topMatch’s optimal timing, meaning calling topKMatches with k = 1 will never be as fast as properly implementing topMatch if written correctly. If your topMatch method simply calls topKMatches with k = 1 and returns the output for either Autocompletor implementation, you will lose points.
###After BinarySearchAutocomplete Is Written
You can test BinarySearchAutocomplete similar to how you tested Term - set AUTOCOMPLETOR_CLASS_NAME to BINARY_SEARCH_AUTOCOMPLETE from AutocompleteMain, and run it using words-333333.txt as the source and “auto” as the query. The results
should be the same as the ones shown on the previous page. In general, BruteAutocomplete and BinarySearchAutocomplete (and TrieAutocomplete) should always produce the same output for topMatch and topKMatches.
Keep in mind that if your BruteAutocomplete works but BinarySearchAutocomplete does not, it may be a problem with Term instead of with BinarySearchAutocomplete - BruteAutocomplete only uses Term.WeightOrder, whereas BinarySearchAutocomplete could potentially use all of Term’s Comparable/Comparators.
Introduction to Tries
You may already have some familiarity with what a trie is, and you should have familiarity with what a tree is. Regardless, completing TrieAutocomplete is very difficult without a mastery of tries, so this page will cover the basics of Tries and their functionality.
###What Is A Trie?
A trie is simply a special version of a tree. In some trees, each node has a defined number of children, and a fixed way to refer to each of them. For example, in a binary tree, each node has two children (each of which could be null), and we refer to these as a left and a right child. Tries are different in that each node can have an arbitrary number of children, and rather than having named pointers to children, the pointers are the values in a key-value map.
So, while a node in a Java binary tree might be defined as
public class Node{
Node myLeft, myRight;
}
A node in a Java trie might look like
public class Node {
Map<Character, Node> children;
}
(Note that the Node class given to you has much more information than this)
The keys of the map will also correspond to some value. For example, for a trie that stores many Strings (as we wish to in this assignment), the keys will be characters. In order to reach the node representing a word in a trie, we simply follow the series of pointers corresponding to the characters in the String. Below is a drawing of a sample word trie:

######From the Wikipedia article on Tries
The top node is the root. It has three children, and to get to these children we have to use the keys t, A, and i. The word each node represents is the concatenation of the keys of pointers you have to take from the root to get to that node. So, to get to “tea” from the root, we have to follow the root’s t pointer, then the e pointer, then the a pointer.
More generally, to get to a node representing a word in the String str, given a root pointer we might use the following code loop:
Node curr = root;
for (int k = 0; k < str.length(); k++) {
curr = curr.children.get( str.charAt(k));
}
###Trie Functionality And Utility
In creating a trie, we will of course have to add values to it. Adding a value to a trie is very similar to navigating to it. To add a value, simply try navigating to that value, but anytime a node on the path to that value is missing, create that node yourself. The code for adding the word in str to a trie might look like this:
Node curr = root;
for (int k = 0; k < str.length(); k++) {
if (!curr.children.containsKey(str.charAt(k))) {
curr.children.put(str.charAt(i), new Node());
}
curr = curr.children.get(str.charAt(i));
}
(Again, please note that the Node class given to you is more detailed and this code alone is not a solution to this assignment)
We use tries because they have some useful properties, which we will take advantage of in this project:
- The time it takes to find an entry in a trie is independent of how many entries are in that trie - more specifically, to navigate to a node corresponding to a word of length w in a trie that stores n words takes O(w) time as opposed to O(f(n)) for some f(n). This improvement is possible because every navigation to the same word passes through the same set of nodes, and thus takes the same time regardless of what other nodes exist.
- All words represented in the subtrie rooted at the node representing some word start with that word. That is, the node representing "apple" will always be below the node representing "app" or more generally, every node below the node representing "app" represents a word starting with "app". For this reason, tries are sometimes called prefix trees. Given that the autocomplete algorithm is searching for words starting with a given prefix, this structure proves very useful.
TrieAutocomplete Overview/Methods
TrieAutocomplete
implements the Autocompletor interface, which means it should, given a list of terms and weights for those terms, be able to find the top match(es) for a prefix amongst those terms. To do this, you will write methods to construct a trie, and then use the trie structure to quickly filter out all terms starting with a given prefix, and then find the highest weighted terms.
Within this class, you should:
- Write the trie method add
- Write the interface-required method topMatch
- Write the interface-required method topKMatches
###The Node Class
For this entire page, it may be useful to have the Node class given to you open for
reading. In addition, you should be comfortable with the basic concepts of a trie at this point.
The Node class comes with several class variables for your use in completing TrieAutocomplete:
###Add
Look at the constructor for TrieAutocomplete. It initialize the trie’s root, and then calls the void add method on every word-weight pair in the arguments for the constructor. Your task is to write the add method such that it constructs the trie correctly. That is, if you write the method correctly, then every word-weight pair should be represented as a trie, and the descriptions of the class variables for Nodes listed above should be true for every node. More specifically, when add is called on a word-weight pair, you should:
To help you understand what all your add method should be doing, here’s an example of a series of adds. In the trie below, each node’s mySubtreeMaxWeight is red, the key to that node is the letter inside of it, and if the node represents a word, it has a green background and its weight is in blue.
We start with just a root:

We call add(“all”, 3). Notice how since the only word at this point has weight 3, all nodes have mySubtreeMaxWeight 3.
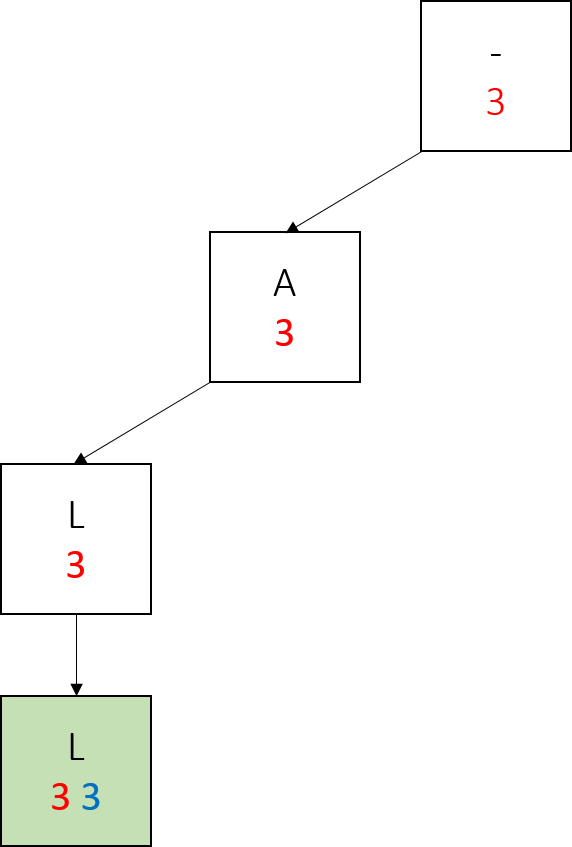
We call add(“bat”, 2). Only the nodes in the right subtree have mySubtreeMaxWeight 2, because the largest weight is still 3.
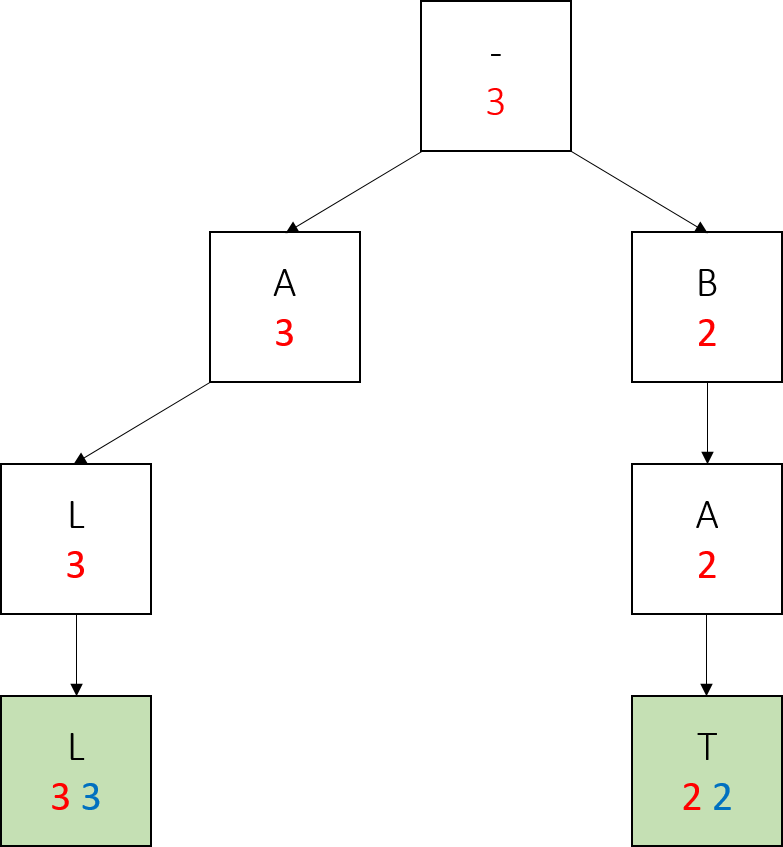
We call add(“apes”, 5). This time, we don’t create a node for the first letter. We update the mySubtreeMaxWeight of the root and the “a” node.
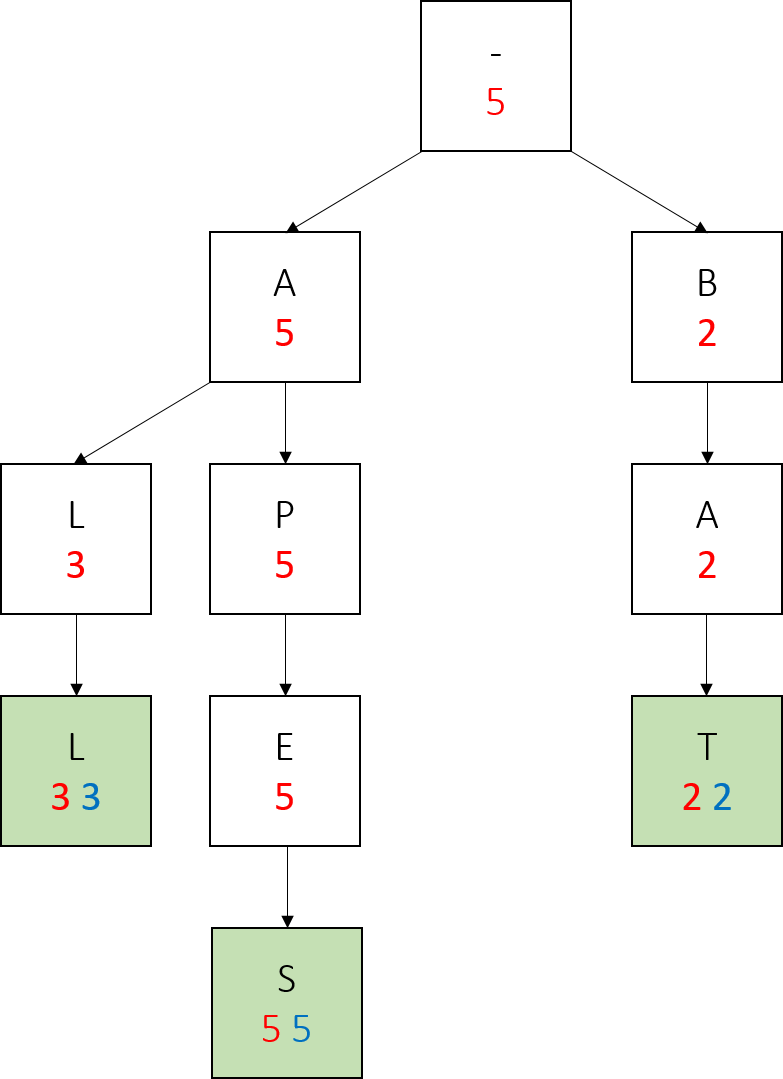
We call add(“ape”, 1). Notice how we create no new nodes, simply modify the values of an existing node.
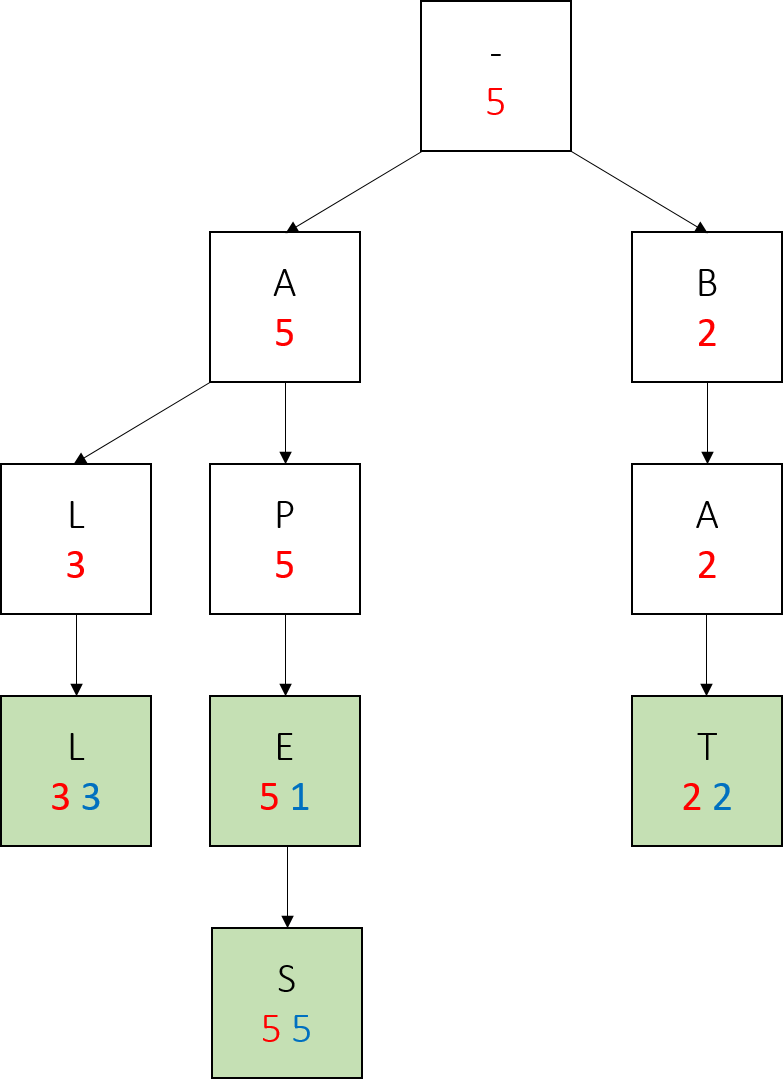
Lastly we call add(“bay”, 4). Notice the changes in red numbers, and that we only created one new node here.
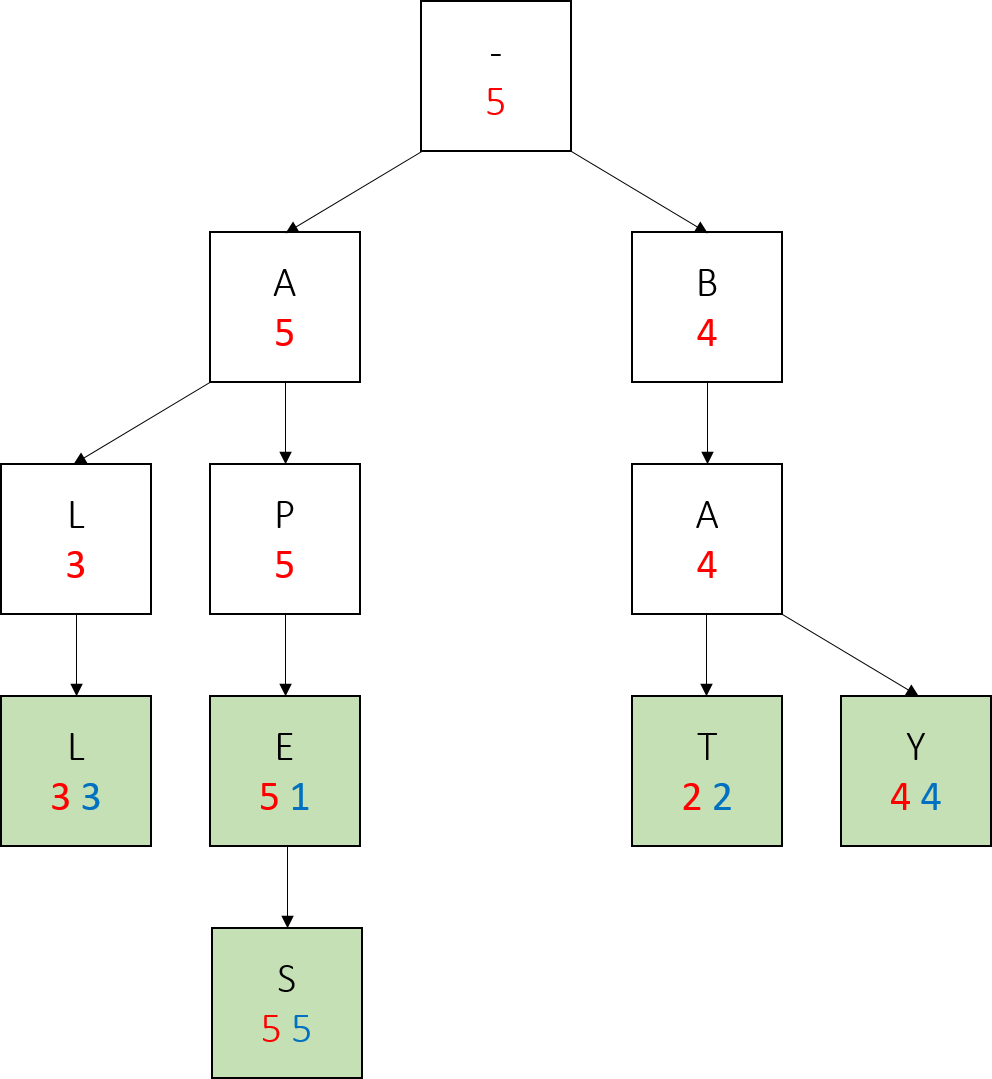
Also note how in the final tree, any word which has no larger-weight words below it (every word but apes) has the same red and blue values. This is true of any trie we construct in this project, if the parameters of nodes are updated correctly - a node with the same myWeight and mySubtreeMaxWeight has no children with a larger weight.
Most importantly, notice how on the path from a node representing a prefix to the largest weighted word in the subtree rooted at that node, all the red values are the same, and this value is also the weight of the largest weighted word. We will take advantage of this fact when writing topMatch().
This example of constructing a trie using add is a more simple one - we never added a word below an existing word, or a word which already exists. Your add should be able to handle any series of calls on word-weight pairs appropriately, including corner cases.
The most notable corner case is adding a word that already in the trie, but with a lower weight - for example, if we were to call add(“apes”, 1). In this case, we would have to update the weight of apes, and then the mySubtreeMaxWeight of all its ancestors. This is especially tricky because not all the ancestors would not have the same new value. Be sure to take advantage of parent pointers when writing code specific to this case.
###TopMatch Fortunately, once add is written topMatch() becomes very simple. As noted in the above example, the mySubtreeMaxWeight of every node from a prefix node to the node under the prefix node with the highest weight will be the same as that highest weight. Thus, the algorithm to find the top match is simply:
###TopKMatches topKMatches() is similar, but not quite the same as topMatch(). We will still be taking advantage of mySubtreeMaxWeight to quickly navigate to high-weight nodes, but this time, we will have to go down multiple branches instead of just one.
To find the top k matches as quickly as possible, we will use what is known as a search algorithm - keep a PriorityQueue of Nodes, sorted by mySubtreeMaxWeight. Start with just the root in the PriorityQueue, and pop Nodes off the PriorityQueue one by one.
Anytime we pop a node off the PriorityQueue, or “visit” it, we will add all its children to the PriorityQueue. Whenever a visited node is a word, add it to a weight-sorted list of words.
When this list has k words with weight greater than the largest mySubtreeMaxWeight in our priority queue, we know none of the nodes we have yet to explore can have a larger weight than the k words we have found. At that point, we can stop searching and return those k words. If we run out of nodes in the PriorityQueue before we find k words, that means there are not k words in the trie.
Benchmarking Autocomplete
The class AutocompleteBenchmark has been provided to you for timing your implementations of Autocompletor. To test a specific implementation, change the return value of the getInstance method to a new instance of the implementation you are testing.
The benchmark class will time all of the following, for a source file you choose through JFileChooser:
You can, of course, modify the benchmark class to add more tests.
For timing method calls, the benchmark class runs until either 1000 trials or 5 seconds have passed (to try to minimize variation in the results) and reports the average. Thus, it should not be surprising if one test takes 5 seconds to run, but if more than 5 seconds pass and a test has not completed, there is likely an infinite loop in your code.
Even for the largest source files (fourletterwords.txt and
words-333333.txt) BinarySearchAutocomplete
and TrieAutocomplete should have some or most methods take times in the range of microseconds. This makes these methods’ runtimes very susceptible to variation, even when we run 1000 trials of them - be sure to consider this when interpreting results and writing your analysis.
Analysis
In addition to submitting your completed classes, you should benchmark them. Then, answer the following questions. Use data wherever possible to justify your answers, and keep explanations brief but accurate:
- What is the order of growth (big-Oh) of the number of compares (in the worst case) that each of the operations in the Autocomplete data type make, as a function of the number of terms N, the number of matching terms M, and k, the number of matches returned by topKMatches for BinarySearchAutocomplete?
- How does the runtime of topKMatches() vary with k, assuming a fixed prefix and set of terms? Provide answers for BruteAutocomplete, BinarySearchAutocomplete and TrieAutocomplete. Justify your answer, with both data and algorithmic analysis.
- Look at the methods topMatch and topKMatches in BruteAutocomplete and BinarySearchAutocomplete and compare both their theoretical and empirical runtimes. Is BinarySearchAutocomplete always guaranteed to perform better than BruteAutocomplete? Justify your answer.
- For all three of the Autocompletor implementations, how does increasing the size of the source and increasing the size of the prefix argument affect the runtime of topMatch and topKMatches? (Tip: Benchmark each implementation using fourletterwords.txt, which has all four-letter combinations from aaaa to zzzz, and fourletterwordshalf.txt, which has all four-letter word combinations from aaaa to mzzz. These datasets provide a very clean distribution of words and an exact 1-to-2 ratio of words in source files.) </ol>
Grading Criteria
For transparency’s sake, below is a list of aspects of your code the automated tests will check. Your code will still be checked by a TA, and passing all these tests does not guarantee a perfect grade.
This may appear to be a large number of tests, but if you follow the guidelines set in the method headers and this writeup, you should already be passing most of, if not all of these tests:
Grading
This assignment is worth 40 points.
- 70% Correctness: for your implementation of Term, BinarySearchAutocomplete, and TrieAutocomplete and passing the tests described above.
- 17.5% Analysis: for your README, data from AutocompleteBenchmark. answers to the questions, and description of the tradeoffs.
- 12.5% Engineering: for your the structure and style of your Autcompletor implementations. Is your code inefficient? </ul>
Credits
The Autocomplete assignment was originally developed by Matthew Drabick and Kevin Wayne of Princeton University for their COS 226 class. The introductory portion of this writeup was based off the writeup for the Princeton version of the assignment, which can be found here.
The assignment was restructured for use at Duke by UTA Austin Lu ’15, UTA Arun Ganesh ‘17, and Prof. Jeff Forbes.
FAQs
####Should I account for capitalization at all?
No, do not worry about capitalization in your Autocompletor implementations. The GUI handles capitalized search terms for you, by translating the search terms and user input into lowercase before passing them to the Autocompletor, and then translating the results back to their original casing for the user display. Thus, it should never be the case when called from the GUI that your Autocompletor has to match lowercase and uppercase terms properly. In addition, our test suites will not ever test for capitalization-based cases.
####Can I use Collections.binarySearch to complete BinarySearchAutocomplete?
You can, but your solution will either be incorrect or inefficient - Collections.binarySearch makes no guarantees about what index it will return if there are multiple matching elements, whereas we specifically need the first or last index. You could use Collections.binarySearch to find the index of one matching element, and then go backwards/forwards until the first/last matching element is found, but this causes your runtime to go from O(log n) to potentially O(n) because you are now doing a linear search.
####When I try to test/benchmark my implementations, nothing happens/it runs forever on a certain test. Why is this?
This will happen if a single method call takes more than a few seconds (unlikely, since BruteAutocomplete can run in <.005s per call and the others should only improve on this time), or if there is an infinite loop. You are most likely to get infinite loops in TrieAutocomplete, since you will often be using while loops or for loops to navigate through the trie. Check the exit conditions of said loops and make sure they are achievable.
####Why do I get a NullPointerException in TrieAutocomplete?
Usually this happens when you go “off” of the trie - that is, try to visit a node that does not exist/is null - and do not realize it/check for it in your code.
Suppose your trie contains the word “ape” but not the word “app” (or anything starting with “app”) and you try to navigate to the node representing “app”. At the node representing “ap”, you would call children.get("p"), but since that node doesn’t exist the call will return null, which can then lead to a NullPointerException if, for example, you try to visit one of its children or look at its weight.
To fix this, before you ever visit a node that isn’t the root, check to make sure that node exists/is not null. If it is null, then react appropriately based on what method you’re currently in.
Note that iterating over the key set of children should never cause a NullPointerException.
####Why should my TrieAutocomplete be able to add a word that already exists?
More than anything this is a test of your ability to traverse a trie using parent pointers, but you can think of it as an ‘update’ method, because as mentioned, real autocomplete implementations need to update the weight of their terms frequently.
Autocomplete
Autocomplete - Overview
Welcome to the Autocomplete assignment. In this assignment, you will be implementing the autocomplete algorithm, which is discussed at length here, using binary search and trie traversal. In doing so, you will see some of the advantages of using tries (or more generally, trees/graphs) and sorted arrays over general arrays.
As always, before starting be sure to snarf the assignment via Ambient so you can read along. You can alternatively download the .jar file here.
You can also view/download the individual classes:
Here is a printer friendly version of this assignment.
###Introduction
In this assignment, you will implement autocomplete for a given set of N terms, where a term is a query string and an associated nonnegative weight. That is, given a prefix, find all queries that start with the given prefix, in descending order of weight.w
For example, if I am given the query “com” I might suggest terms like “computer”, “communication” or “combine”. For this assignment, our terms have predetermined fixed weights assigned to them, and we will return the highest-weighted terms among those terms that share have the query as their prefix.
In this assignment, you will:
- Complete a datatype
Termthat represents an autocomplete term: a query string and an associated real weight. - Write a class,
BinarySearchAutocompletethat impletements autocomplete functionality by using binary search to find the all query strings that start with a given prefix; and sort the matching terms in descending order by weight. - Write a class,
TrieAutocompleteto implement Autcocomplete functionality using a Trie data structure. </ol> When you snarf this project, you will receive the following already completed classes:Autocompletor– the interface which you will be writing implementations of.AutocompleteMain– the class to launch the GUI from. When testing your implementations of autocomplete, you will need to change the String AUTOCOMPLETOR_CLASS_NAME’s value.AutocompletorBenchmark– once you have written an implementation of Autocompletor, this class will tell you how quickly it runs.BruteAutocomplete- A completed (albeit slow) implementation of Autocompletor.Node– a node class for use in TrieAutocomplete. Nothing needs to be modified here, but definitely read through this class before starting TrieAutocomplete.AutocompleteGUI– the GUI for this project. You can ignore this class.
Term– a class used to encapsulate individual search terms and their weights, which includes several methods of comparing terms. You need to complete these class in order for BruteAutocomplete to be usable with AutocompleteMain.BinarySearchAutocomplete– an implementation of Autocompletor which performs the autocomplete algorithm using binary search.TrieAutocomplete– an implementation of Autocompletor which performs the autocomplete algorithm using trie exploration.
Autocompletorimplementations:-
TestTerm,TestBinarySearchAutocomplete, andTestTrieAutocompleteto test the correctness; and -
AutocompleteBenchmarkto analyze the efficiency.